Mixed-integer linear programming approaches for tree partitioning of power networks
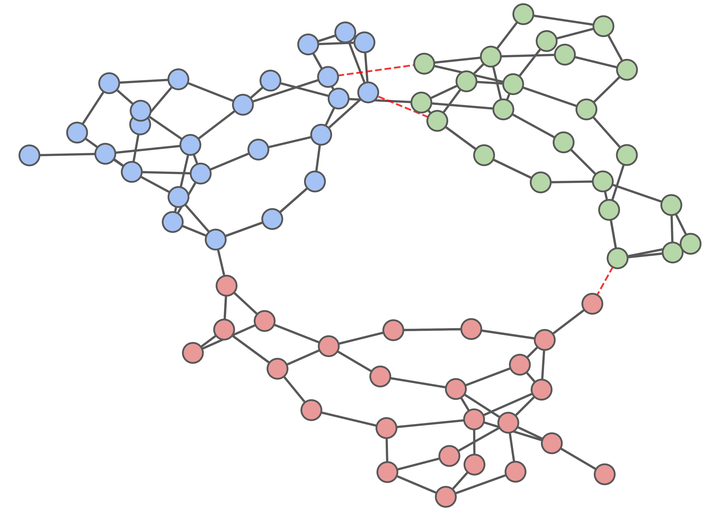 A tree-partitioned IEEE-73 network after the removal of three transmission lines (in red).
A tree-partitioned IEEE-73 network after the removal of three transmission lines (in red).
Abstract
In transmission networks, power flows and network topology are deeply intertwined due to power flow physics. Recent literature shows that a specific more hierarchical network structure can effectively inhibit the propagation of line failures across the entire system. In particular, a novel approach named tree partitioning has been proposed, which seeks to bolster the robustness of power networks through strategic alterations in network topology, accomplished via targeted line switching actions. Several tree partitioning problem formulations have been proposed by considering different objectives, among which power flow disruption and network congestion. Furthermore, various heuristic methods based on a two-stage and recursive approach have been proposed. The present work provides a general framework for tree partitioning problems based on mixed-integer linear programming (MILP). In particular, we present a novel MILP formulation to optimally solve tree partitioning problems and also propose a two-stage heuristic based on MILP. We perform extensive numerical experiments to solve two tree partitioning problem variants, demonstrating the excellent performance of our solution methods. Lastly, through exhaustive cascading failure simulations, we compare the effectiveness of various tree partitioning strategies and show that, on average, they can achieve a substantial reduction in lost load compared to the original topologies.